C++ 实现梯度下降法解多元线性回归

两个宝贝

1 线性回归

在统计学中，线性回归（英语：linear regression）是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归（multivariable linear regression）。
2 输入和输出

多元线性回归中，一个因变量由 m 个自变量决定，那么假设函数为
h(X) = \theta ^ {T} X = \sum_{j = 0}^{m} \theta_j x_j
我们的目标就是根据 (X|Y) 找到合适的 \theta，使得回归后的残差最小。
那么我们的输入就确定为 (X|Y)，输出确定为 \theta
3 代价函数

代价函数 J(\theta) 表示了使用某一特定 \theta 回归的效果。代价函数值越小，则说明回归效果越好。那么，我们的目标是最小化代价函数，而用到的工具就是梯度下降。
J(\theta) = \frac{1} {2n} \sum_{i =1}^{n}(h(X_i) -y_i)^2 \\  J(\theta)= \frac{1} {2n} \sum_{i =1}^{n}(\sum_{j = 0}^{m} \theta_j x_{ij} -y_i)^2
4 梯度下降




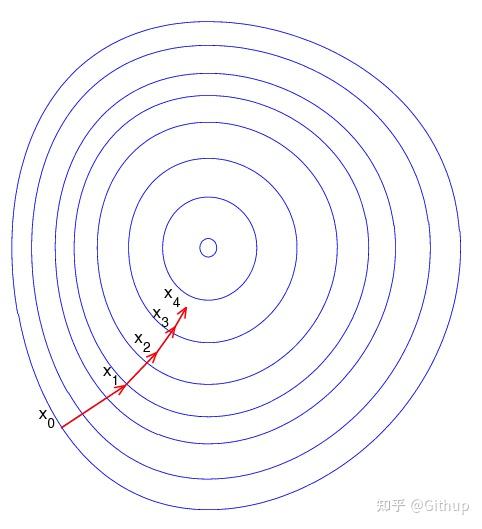
梯度下降法（英语：Gradient descent）是一个一阶最优化算法

我们使用梯度下降算法不断迭代 \theta 直至 J(\theta) 收敛。
\theta_j := \theta_j -  \alpha \frac {\partial} {\partial \theta_j} J(\theta)
其中：
\frac {\partial} {\partial \theta_j} J(\theta)  = \frac {1} {n} \sum_{i = 1} ^ {n}(h(X_i) - y_i)x_{ij}
\alpha 为学习率
5 C++ 实现

typedef long double Data;
typedef std::vector<Data> DataVector;
typedef std::vector<DataVector> DataMatrix;
a. 假设函数
Data hypothetical(const DataVector &Xi, const DataVector &theta) {
    int m = Xi.size();
    if (theta.size() != m) {
        std::cerr << "hypothetical: the size is not matched." << std::endl;
        return {};
    }
    Data h = 0;
    for (size_t j = 0 ; j < m ; j ++ ) {
        h += Xi[j] * theta[j];
    }
    return h;
}
b. 代价函数
Data costFunction(const DataMatrix &X, const DataVector &Y, const DataVector &theta) {
    size_t n = X.size();
    Data J = 0;
    for (size_t i = 0 ; i < n ; i ++ ) {
        J += powl(hypothetical(X, theta) - Y, 2);
    }
    J /= (Data) (2 * n);
    return J;
}
c. \frac {\partial} {\partial \theta_j} J(\theta)  
Data costFunctionDerivation
    (const DataMatrix &X, const DataVector &Y, const DataVector &theta, size_t j) {
    size_t n = X.size(), m = X[0].size();
    Data derivation = 0;
    for (size_t  i = 0 ; i < n ; i ++ ) {
        derivation += (hypothetical(X, theta) - Y) / n * X[j];
    }
    return derivation;
}
d. 多元线性回归
DataVector multipleLinearRegression
    (const DataMatrix &X, const DataVector &Y,
    Data learningRate) {

    size_t n = X.size();
    if (Y.size() != n) {
        std::cerr << "multipleLinearRegression: the size is not matched." << std::endl;
        return {};
    }
    size_t m = X[0].size();
    DataVector theta;
    for (size_t j = 0 ; j < m ; j ++ ) {
        theta.push_back(0);
    }

    size_t counter = 0;

    while (true) {
        Data old = costFunction(X, Y, theta);
        for (size_t j = 0 ; j < m ;  j ++ ) {
            Data cd = costFunctionDerivation(X, Y, theta, j);
            theta[j] = theta[j] - learningRate * cd;
        }
        Data current = costFunction(X, Y, theta);
        counter ++;
        if (old == current) {break;}
    }

    std::cout << "counter: " << counter << std::endl;

    return theta;
}
测试用例
(X|Y)= \begin{array}{} 1 & 1 & 3.9 \\ 1 & 2 & 7.1 \\ 1 & 3 & 10.1 \\ 1 & 4 & 12.9 \end{array}
运行结果


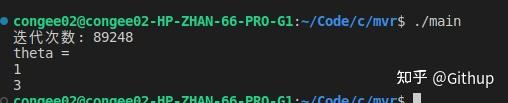
完整代码
https://gitee.com/zhouluji/multiple_linear_regression